Чіпаємо нескінченність. Мебіус, Клейн та інші топологічні парадокси. Завдання. Пізнавальні статті і незвичайні фотографії.

1. Односторонні поверхні: Лист Мебіуса і Пляшка Клейна Ми так часто чуємо слово - Нескінченність, а...
2. Фокус №1
3. Фокус №2
4. Фокус №3
5. Фокус№4
6. ЮФокус №5
7. Виникає логічне запитання: Чи існують ще подібні об'єкти?
8. Ось - звичайна Пляшка Клейна:

Односторонні поверхні: Лист Мебіуса і Пляшка Клейна

Ми так часто чуємо слово - Нескінченність, а чи не хотілося вам коли ні будь потримати цю саму нескінченність в своїх руках? Для того що б зробити це вам доведеться взяти в руки папір, ножиці і клей. Відріжте смужку паперу і склейте її як показано на малюнку.

У Вас вийшла така одностороння поверхню:

кільце Мебіуса

Що значить одностороння? Це означає, що мураха (або житель Плоскатіі, про який ми говорили в попередній статті) побуває на обох сторонах цього листа не переходячи через край. Це означає, що ви можете не відриваючи олівця від паперу, і не переходячи через край зафарбувати цю фігуру з обох сторін.

Якщо вам здається що нічого особливого в цьому немає, тоді спробуйте вирішити наступну головоломку:

Це давня головоломка про трьох колодязях і трьох будинках.

В ряд стоять 3 будинки, навпроти кожного з них є по колодязя. Потрібно від кожного будинку зробити стежки до кожного з колодязів так, що б ніякі 2 стежки не перетиналися.

Нижче ви можете зробити це в динаміці, тільки колодязі тут замінені: Газом, Водою і Електрикою. Потрібно до кожного з будинків провести і газ і воду і електрику, і що б не якісь 2 труби (електричні кабелі) не перетиналися.

Ну як? Не виходить?

Не так давно була доведена нерозв'язність цієї задачі за допомогою формули Ейлера (див. Замітку на нашому сайті " Прогулянка по мостах ").

Але завдання це не розв'язна на ПЛОЩИНІ, НА ПАПЕРІ.

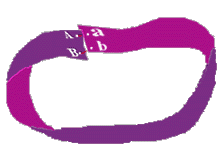
Хіба ми з вами живемо на папері? Нас зі школи вчили оперувати поняттями «евклідовой геометрією», а по простому - нас зі школи вчили мислити «Плоско». Що ж стосується цієї головоломки, то вона має рішення, тільки не в придуманому, а в реальному світі. У цьому нам допоможе Лист Мебіуса. З'єднайте відповідні букви, і отримаєте відповідь на головоломку.

Зрозуміло, це тільки початок. Лист Мебіуса таїть в собі ще багато несподіванок.

Фокус №1

Зробіть ще один Лист Мебіуса, повернений на підлогу обороту (180 градусів). А тепер спробуйте його розрізати посередині.

Я Вам не скажу що вийде так як:
а) Якщо Ви вже тримаєте в руках Лист Мебіуса і ножиці, то позбавити Вас задоволення спостерігати за тим, що станеться після розрізання - це просто злочин.
б) Якщо Ви і не думали брати в руки ножиці - тоді сказаний мною результат вас не здивує.

Ну як вийшло? Зверніть увагу, на скільки оборотів закручений одержаний примірник?

Фокус №2

Закрутіть Лист на 2 півоберту (360 градусів), і розріжте його посередині. Що виходить?

Фокус №3

Виготовте Лист Мебіуса, який закручений на підлогу обороту (180 градусів), і починайте його розрізати відступаючи весь час одну третину від краю.

Що виходить на цей раз?

Фокус№4

Тепер виготовте Лист Мебіуса, який закручений на 3 півоберту (540 градусів), і розріжте його навпіл. У вас повинен вийти Лист Мебіуса, який закручений вузлом. Начебто цього, але складніше:

ЮФокус №5

Цікаві речі так само вийдуть, якщо скласти папір гармошкою, потім скрутити з неї Лист Мебіуса і різати навпіл, або відступаючи одну третину. Насамперед зробіть гармошку, яка складається з одного перегину, утворіть лист Мебіуса поворотом на 360 градусів, і розріжте посередині. Перед вами постануть 3 зчеплених між собою кільця.

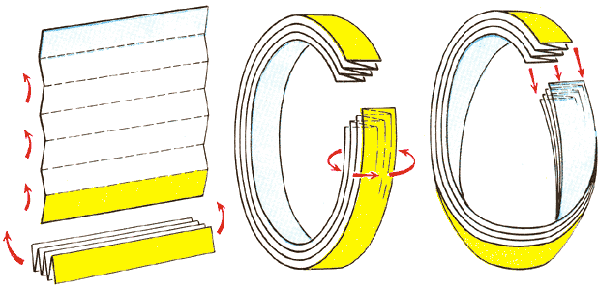
Ви робите нові і нові Листи, але ж не кожного смужку можна скрутити в Лист Мебіуса. Наприклад, з квадратного аркушу паперу Лист Мебіуса не вийде. Тоді яке повинно бути мінімально відношення довжини до ширини смужки, що б з неї можна було склеїти Лист Мебіуса?

Приймемо для ясності ширину смужки за 1. Виявляється, що мінімальна довжина смужки дорівнює v3, це приблизно 1,73. Отримане значення дорівнює другому «Золотому перетину».

Виникає логічне запитання: Чи існують ще подібні об'єкти?

Так, існують, і ще більш хитромудрі. Якщо Лист Мебіуса - «умовно двовимірний об'єкт» (він отриманий з плоскою смужки), то його подружка - Пляшка Клейна повноправно займає 3 вимірювання. Ось як вона виглядає:

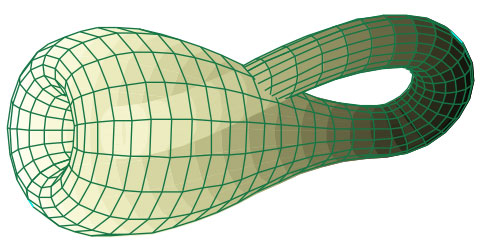
Пляшка Клейна - 3D подружка плоского Мебіуса

Запустіть суду мурашки, і бідолаха побуває у всіх точках Пляшки Клейна - не роблячи в ній дірок, і не переповзаючи через край.

На всіх малюнках показано наступне: в місці, де трубка «проникає в пляшку» - немає зазору, хоча це не правильно! Адже якщо немає зазору, тоді мураха повинен буде виповзати з пляшки тим же маршрутом, яким він туди вповзав. Хіба блукаючи по Лісту Мебіуса йому потрібно було розвертатися після того як він кудись дійшов? Нескінченність, вона на те й нескінченність!

А чому ми тільки обходимо Пляшку Клейна? Адже Лист Мебіуса ми різали вздовж і впоперек. Що ж буде якщо розрізати Пляшку Клейна?

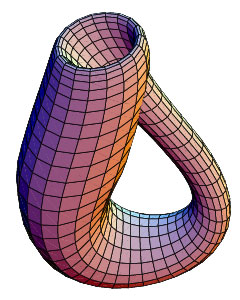
Це неймовірно, але вийшов Лист Мебіуса. Різати, правда, потрібно було так, що б ріжучий предмет робив оборот в 360 градусів між початковою точкою і кінцевої.

Пляшка Клейна в трьох вимірах - це аналог Ліста Мебіуса в двох вимірах. Вище ви бачили «багатошаровий» Лист Мебіуса - отриманий склеюванням паперу складеної «гармошкою». А чи існують «Багатошарові» Пляшки Клейна? Як виявилося - існують. Назвемо їх - Пляшки Макса (придумав автор статті - Максим К.).

Ось - звичайна Пляшка Клейна:

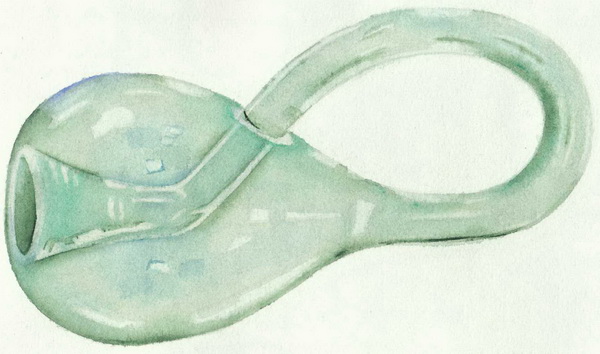
А тепер подумки уявіть собі, як всередині цієї пляшки починає формуватися нова Пляшка Клейна. Спочатку всередині утворюється «Пляшка Клейна» без «трубки» - пляшка з двома отворами, потім утворюється трубка, яка проникає в «трубку» іcходной «Пляшки Клейна», проходить всю «трубку», проникає через отвір в тільки що сформувалася «Пляшка Клейна» . Потім трубка проникає в друге отвір основний «Пляшки Клейна». Перебуваючи в задній частині основної пляшки, «трубка» починає повільно обволікати вихідну «Пляшка Клейна» перетворюючись при цьому в третю, найбільшу «Пляшка Клейна».

Процес доходить до «трубки» - споконвічній «Пляшки Клейна», і поступово огортає її, потім ця «трубка» проникає тільки що сформувалася «Пляшка Клейна», потім у вихідну, потім в найменшу. Проникнувши в найменшу «Пляшка Клейна», «трубка» доходить до отвору і зливається з ним.

Вийшло що найменша «Пляшка Клейна» перейшла в найбільшу, і стала з нею одним цілим. Нижче малюнок того, що ви намагалися уявити.

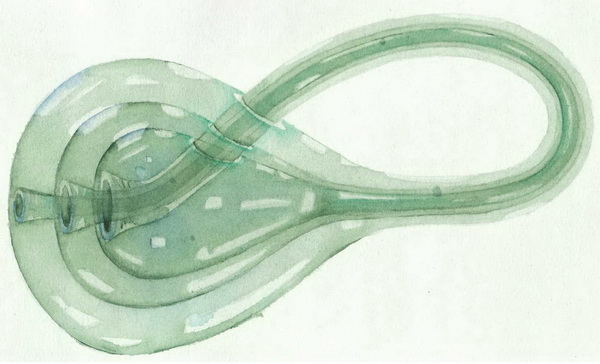
Не обов'язково розуміти цей світ, потрібно лише знайти себе в ньому - Альберт Ейнштейн

І все ж, чи так уже потрібно ламати голову над тим, як влаштований цей світ? Або все що нам потрібно вже є, і нам залишається лише вибрати «правильний» варіант? Вибір як завжди за вами. Він у вас є навіть в тому - робити цей вибір чи ні.

За матеріалами: СОЗЕРЦАЕМ.COM.UA

Dmitry 21.04.2009