6. Наближена квадратура кола у народів Середньої Азії і Близького Сходу
Середньоазіатські народи мають за своїми плечима багату самобутню культуру, коріння якої сягають у глибину віків. Особливо великий внесок внесли середньоазіатські вчені в світову математичну культуру, будучи зачинателями ряду наукових математичних дисциплін і особливо астрономії, алгебри, тригонометрії.
Історичні дослідження останніх років показують, що перше місце в розвитку математики в країнах арабського халіфату на протязі більше 500 років, з IX по XVI ст., Незмінно належало вченим народів Середньої Азії і Закавказзя і перш за все таджиків, узбеків і азербайджанцям. Має рацію А. П. Юшкевич, підкреслюючи, що "Досягнення середньоазіатських математиків IX-XV ст. Належать, таким чином, в переважній своїй частині народам нашої країни і тому повинні привернути особливу увагу радянських істориків науки" (А. П. Юшкевич, Про математики народів Середньої Азії в IX-XV ст., "Історико-математичні дослідження", вип. 4, ГІТТЛ, 1951, стор. 45).
З ранніх середньоазіатських вчених багато займався наближеною квадратурою кола відомий хорезмійський алгебраїст першої третини IX ст. ал-Хорезмі (Мухамед бен Муса ал-Хорезмі), яка прославила себе двома трактатами: один з алгебри "Хісаб ал-джебр вал-мукабала", а інший з арифметики "Арифметика" ал-Хорезмі.
Ал-Хорезмі жив при дворі халіфа ал-Мамуна, покровителя і цінителя наук, за велінням якого перекладалися давньогрецькі класики ( "Начала" Евкліда, "Конічні перетину" Аполлонія і роботи Архімеда "Про вимір кола", "Про кулі і циліндрі", " Алмагест "Птоломея і багато інших), а також вилучення з робіт індійських вчених Аріабхата і Брамагупти. Ал-Хорезмі успішно займався питаннями астрономії (уточнив таблиці хорд Птолемея) і брав участь при вимірюванні градуса земного меридіана. Ал-Хорезмі залишив ще ряд трактатів, в тому числі "Трактат по астролябії" і "Трактат про сонячний годинник".
Своїми творами ал-Хорезмі багато сприяв поширенню індійської системи числення, без якої навряд чи можна було б в Європі отримати "лудольфово число", а також інші, більш точні європейські наближення числа π.
Ал-Хорезмі познайомив свої і європейські народи з найбільш важливими грецькими і індійськими приближениями числа & 3960 ;. Він знайомив читача з архімедовим числом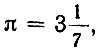 
і підкреслював, що це число є "найбільш вживаним в практиці". Про індійських наближеннях числа π, якими є 
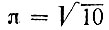і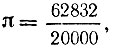 
він говорить як про найбільш точних результатах і підкреслює їх індійське походження.
У так званої "арабської" літературі є твір "Про квадратуру кола" математика ал-Хайтама (помер в 1038), яке цілком присвячене квадратуру кола, але, на жаль, воно ще досі широко не оприлюднене. Один із знавців історії квадратури кола професор Ф. Рудіо висловлює жаль з приводу того, що цей твір "ще ніким не досліджено, тим часом як це перше, відоме нам з часів Архімеда, твір з такою назвою і, судячи з імені автора, слід очікувати знайти в ньому цікаві спроби підійти якомога ближче до площі кола "(Ф. Рудіо, Про квадратуру кола з викладом історії питання. Переклад з німецької, під редакцією і з примітками акад. С. Н. Бернштейна, изд. 3-тє, ОНТИ НКТП СРСР, М.-Л., 1936, стор. 39).
У XV в. наближеною квадратурою кола успішно "займався іранський математик ал-Каші (Джемшид Гіяседдін ал-Каші), що присвятив цьому питанню" Трактат про окружності ".
Віддаючи данину релігійним забобонам, ал-Каші начищає свій трактат так: "Хвала Аллаху, що володіє знанням відносини діаметра до окружності, знає величину всього складного і простого, творцеві землі і небес, творцеві світу у темряві". Говорячи про мету свого твору, Цв передмові до нього він писав: "... ми хочемо так визначити коло кола в частинах, в яких виражений діаметр, щоб ми були впевнені, що в колі, діаметр якого дорівнює шістсот тисяч діаметрів землі, різниця між рей (отриманої величиною окружності) і істинної була не більшою волоса, т. е. Одна шоста ширини середнього (ячмінного зерна, так що різниця для кола менше ніж цей виміряти б нічим (з цих заходів) (Джемшид Гіяседдін ал-Каші, Ключ арифметики і трактат про окружності, Переклад з арабської Б. А. Ро зенфельда, редакція Б. А. Сегала і А. П. Юшкевича, ГІТТЛ, М., 1956, Ігор. 266).
В "Трактаті про окружності" ал-Каші дає наближене обчислення числа 2а з 17 десятковими знаками, висловлюючи це число дробом зі знаменником 1016. Отриманий ал-Каші результат можна записати так:
Цей результат вірний у всіх розрядах.
